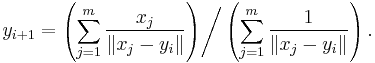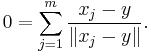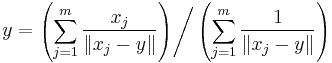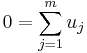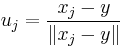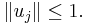Geometric median
The geometric median of a discrete set of sample points in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency in higher dimensions. It is also known as the Fermat–Weber point or 1-median.[1]
The geometric median is an important estimator of location in statistics. It is also a standard problem in facility location, where it models the problem of locating a facility to minimize the cost of transportation.
The special case of the problem for three points in the plane (that is, m = 3 and n = 2) is sometimes also known as Fermat's problem; it arises in the construction of minimal Steiner trees, and was originally posed as a problem by Pierre de Fermat to Evangelista Torricelli, who solved it. Its solution is now known as the Fermat point of the triangle formed by the three sample points. Alfred Weber's name is associated with the more general Fermat–Weber problem due to a discussion of the problem in his 1909 book on facility location.
Wesolowsky (1993) provides a survey of the problem. See Fekete, Mitchell, and Beurer (2003) for generalizations of the problem to non-discrete point sets.
Contents |
Definition
Formally, for a given set of m points 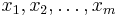 with each
with each 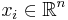 , the geometric median is defined as
, the geometric median is defined as
- Geometric Median
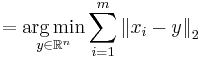
Note that argmin means the value of the argument  which minimizes the sum. In this case, it is the point
which minimizes the sum. In this case, it is the point  from where the sum of all Euclidean distances to the
from where the sum of all Euclidean distances to the  's is minimum.
's is minimum.
Properties
- For the 1-dimensional case, the geometric median coincides with the median. This is because the univariate median also minimizes the sum of distances from the points.
- The geometric median is unique whenever the points are not collinear.
- The geometric median is equivariant for Euclidean similarity transformations, including translation and rotation. This means that one would get the same result either by transforming the geometric median, or by applying the same transformation to the sample data and finding the geometric median of the transformed data. This property follows from the fact that the geometric median is defined only from pairwise distances, and doesn't depend on the system of orthogonal Cartesian coordinates by which the sample data is represented. In contrast, the component-wise median for a multivariate data set is not in general rotation invariant, nor is it independent of the choice of coordinates.
- The geometric median has a breakdown point of 0.5.[2] That is, up to half of the sample data may be arbitrarily corrupted, and the median of the samples will still provide a robust estimator for the location of the uncorrupted data.
Special cases
- For 3 points, if any angle of the triangle is more than 120° then the geometric median is the point making that angle. If all the angles are less than 120°, the geometric median is the point inside the triangle which subtends an angle of 120° to all three pairs of points. This is also known as the Fermat point of the triangle formed by the three points.
- For 4 coplanar points, if one of the four points is inside the triangle formed by the other three points, then the geometric median is that point. Otherwise, the points form a convex quadrilateral and the geometric median is the crossing point of the diagonals of the quadrilateral. The geometric median of four coplanar points is the same as the unique Radon point of the four points.
Computation
Despite being an easy to understand concept, computing the geometric median poses a challenge. The centroid or center of mass, defined similarly to the geometric median as minimizing the sum of the squares of the distances to each sample, can be found by a simple formula — its coordinates are the averages of the coordinates of the samples — but no such formula is known for the geometric median, and it has been shown that no explicit formula, nor an exact algorithm involving only arithmetic operations and kth roots can exist in general. Therefore only numerical or symbolic approximations to the solution of this problem are possible under this model of computation.[3]
However, it is straightforward to calculate an approximation to the geometric median using an iterative procedure in which each step produces a more accurate approximation. Procedures of this type can be derived from the fact that the sum of distances is a convex function, since the distance to each sample point is convex and the sum of convex functions remains convex. Therefore, procedures that decrease the sum of distances at each step cannot get trapped in a local optimum.
One common approach of this type, called Weiszfeld's algorithm,[4] is a form of iteratively re-weighted least squares. This algorithm defines a set of weights that are inversely proportional to the distances from the current estimate to the samples, and creates a new estimate that is the weighted average of the samples according to these weights. That is,
Bose et al. (2003) describe more sophisticated geometric optimization procedures for finding approximately optimal solutions to this problem. As Nie, Parrilo & Sturmfels (2008) show, the problem can also be represented as a semidefinite program.
Implicit formula
If y is distinct from all the given points, xj, then y is the geometric median if and only if it satisfies:
This is equivalent to:
which is closely related to Weiszfeld's algorithm.
If y is equal to some of the given points, then y is the geometric median if and only if there are vectors uj such that:
where for xj ≠ y,
and for xj = y,
Generalizations
The geometric median can be generalized from Euclidean spaces to general Riemannian manifolds (and even metric spaces) using the same idea which is used to define the Fréchet mean on a Riemannian manifold. Let  be a Riemannian manifold with corresponding distance function
be a Riemannian manifold with corresponding distance function 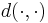 , let
, let  be
be  weights summing to 1, and let
weights summing to 1, and let  be
be  observations from
observations from  . Then we define the weighted geometric median
. Then we define the weighted geometric median  (or weighted Fréchet median) of the data points as
(or weighted Fréchet median) of the data points as
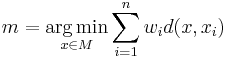 .
.
If all the weights are equal, we say simply that  is the geometric median.
is the geometric median.
See also
- Central tendency
- Centroid, which minimizes the sum of squares of Euclidean distance
- mean
- Fréchet mean
Notes
- ^ The more general k-median problem asks for the location of k cluster centers minimizing the sum of distances from each sample point to its nearest center.
- ^ Lopuhaä and Rousseeuw (1991).
- ^ Bajaj (1986), Bajaj (1988). Earlier, Cockayne and Melzak (1969) proved that the Steiner point for 5 points in the plane cannot be constructed with ruler and compass
- ^ Weiszfeld (1937); Kuhn (1973); Chandrasekaran and Tamir (1989).
References
- Bajaj, C. (1986). "Proving geometric algorithms nonsolvability: An application of factoring polynomials". Journal of Symbolic Computation 2: 99–102. doi:10.1016/S0747-7171(86)80015-3.
- Bajaj, C. (1988). "The algebraic degree of geometric optimization problems". Discrete and Computational Geometry 3: 177–191. doi:10.1007/BF02187906.
- Bose, Prosenjit; Maheshwari, Anil; Morin, Pat (2003). "Fast approximations for sums of distances, clustering and the Fermat–Weber problem". Computational Geometry: Theory and Applications 24 (3): 135–146. doi:10.1016/S0925-7721(02)00102-5. http://www.scs.carleton.ca/~jit/publications/papers/bmm01.ps.
- Chandrasekaran, R.; Tamir, A. (1989). "Open questions concerning Weiszfeld's algorithm for the Fermat-Weber location problem". Mathematical Programming, Series A 44: 293–295. doi:10.1007/BF01587094.
- Cockayne, E. J.; Melzak, Z. A. (1969). "Euclidean constructability in graph minimization problems". Mathematics Magazine 42 (4): 206–208. doi:10.2307/2688541. JSTOR 2688541.
- Fekete, Sándor P.; Mitchell, Joseph S. B.; Beurer, Karin (2003). "On the continuous Fermat-Weber problem". arXiv:cs.CG/0310027 [cs.CG].
- Fletcher, P. Thomas; Venkatasubramanian, Suresh; Joshi, Sarang (2009). "The Geometric Median on Riemannian Manifolds with Application to Robust Atlas Estimation". Neuroimage 45 (1 Suppl): s143–s152. doi:10.1016/j.neuroimage.2008.10.052. PMC 2735114. PMID 19056498. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2735114.
- Kuhn, Harold W. (1973). "A note on Fermat's problem". Mathematical Programming 4 (1): 98–107. doi:10.1007/BF01584648.
- Lopuhaä, Hendrick P.; Rousseeuw, Peter J. (1991). "Breakdown points of affine equivariant estimators of multivariate location and covariance matrices". Annals of Statistics 19 (1): 229–248. doi:10.1214/aos/1176347978. JSTOR 2241852.
- Nie, Jiawang; Parrilo, Pablo A.; Sturmfels, Bernd (2008). "Semidefinite representation of the k-ellipse". In Dickenstein, A.; Schreyer, F.-O.; Sommese, A.J.. Algorithms in Algebraic Geometry. IMA Volumes in Mathematics and its Applications. 146. Springer-Verlag. pp. 117–132. arXiv:math/0702005.
- Ostresh, L. (1978). "Convergence of a Class of Iterative Methods for Solving Weber Location Problem". Operations Research 26 (4): 597–609. doi:10.1287/opre.26.4.597.
- Weber, Alfred (1909). Über den Standort der Industrien, Erster Teil: Reine Theorie des Standortes. Tübingen: Mohr.
- Wesolowsky, G. (1993). "The Weber problem: History and perspective". Location Science 1: 5–23.
- Weiszfeld, E. (1937). "Sur le point pour lequel la somme des distances de n points donnes est minimum". Tohoku Math. Journal 43: 355–386.